Mục tiêu

Khái quát chung về chia để trị

Chia để trị là 1 phương pháp áp dụng cho các bài toán có thể giải quyết bằng cách chia nhỏ ra thành các bài toán con từ việc giải quyết các bài toán con này. Sau đó lời giải của các bài toán nhỏ được tổng hợp lại thành lời giải cho bài toán ban đầu.

Nguyên lí hoạt động của thuật toán Quick Sort

QuickSort hay Sắp xếp nhanh là thuật toán xây dựng dựa trên tư tưởng “Chia để trị” nhắc đến bên trên. 

Đầu tiên ta chọn một phần tử chốt, sau đó so sánh từng phần tử của danh sách với phần tử chốt này để tạo ra 2 phần:

Cứ tiếp tục chia như vậy cho đến khi ta chia ra các dãy con có độ dài bằng 1

Phần tử Pivot là gì? Liên hệ với độ khó thuật toán ? Tại sao độ khó trung bình là O(NlogN) và tệ nhất là O(n^2)

Phần tử chốt (Pivot) được nhắc đến bên trên là phần tử ta sẽ chọn theo từng lần chia để để tạo các danh sách con nhỏ hơn/ lớn hơn phần tử chốt.

Thông thường, ta có 3 cách chọn sau :

Bằng việc chọn phần tử chốt, ta sẽ chia dần dãy ra thành các danh sách con nhỏ hơn/ lớn hơn phần tử chốt.

Trong trường hợp tốt: Ta chọn được phần tử chốt mà chia được dãy thành 2 phần bằng nhau hoặc tương đương, vì vậy ta chỉ cần log(2, N) để chia dãy. Và vì mỗi lần ta lại duyệt qua cả dãy, nên độ khó thuật toán là O(NlogN) (Nxlog(2,N))

Trong trường hợp xấu : Ta chọn phải những phần tử chốt lớn nhất hoặc bé nhất dãy, lúc này danh sách con chia ra thì 1 bên chỉ có 1 phần tử, bên còn lại có n-1 phần tử, và nếu cứ như vậy ta cần chia N lần mới xong. Nên độ khó lúc này là O(n^2)

Vậy có thể thống kê độ khó thuật toán QuickSort như sau :

Thuật toán tìm kiếm nhị phân

Hãy tưởng tượng bạn đang cần tìm tên Nguyễn Quốc Hưng trong một cuốn danh bạ điện thoại dày cộp không có mục lục.

Lật từng trang để tìm lúc này tìm có vẻ thật bất khả thi, trong trường hợp xấu nhất, nếu tên Nguyễn Quốc Hưng ở cuối và ta lật từ đầu, vậy ta phải lật hết N trang của cuốn sách O(N)

Liệu có cách nào nhanh hơn không ?

Thực ra trong thực tế, ta đã luôn vô thức làm cách nhanh hơn. Bạn có thể chỉ cần chọn 1 trang ở giữa, bên trong là tên Ngọc Tâm, T > H, lúc này bạn biết hiện tại là ở vùng chữ T, và Hưng (H) không thể xuất hiện ở những trang phía sau nữa được, và ta chỉ cần tìm ngược lại phía trước. Lật 1 trang sách thấy tên của Hoàng Dương (D), ta biết H không thể ở phía trước D, vì vậy ta chỉ cần tìm tiếp trong phần tiếp theo của chữ D.

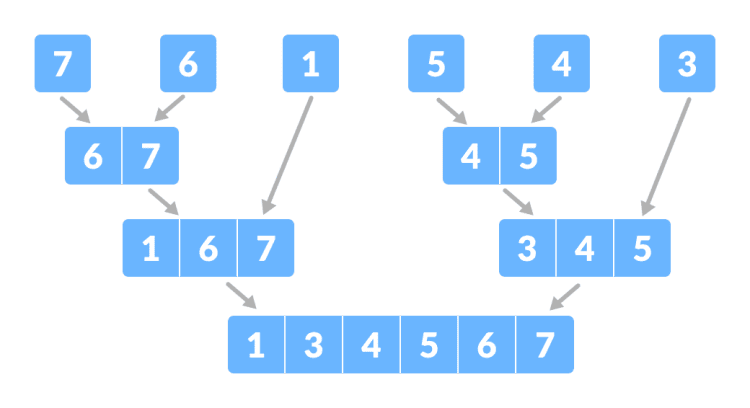
Hình ảnh minh họa:

Ta cần tìm kiếm số 6

chỉ-mục-giữa = (cuối + đầu)/ 2

Bước 1 : Chọn phần tử ở giữa (số 4), 4 < 6, vậy số 6 chỉ có thể ở vùng bên trái số 4 (những số lớn hơn số 4)

Bước 2 : Chọn phần tử ở giữa ở vùng còn lại lúc này (số 7) , 7 > 6, vậy 6 phải ở bên phải

Lúc này vùng thỏa mãn chỉ còn 1 phần tử, và đó là 6

Do cần chia 2 lần lặp lại, vậy ta chỉ cần chia log(2,N) lần để tìm ra số cần tìm, vậy độ khó của thuật toán tìm kiếm nhị phân là O(logN)

Giải thích Code 2 bài Số bé thứ k, Help Sudo

1. Số bé thứ K

Cho 1 dãy số nguyên. Bạn hãy tìm phần tử ở vị trí thứ k sau khi sắp xếp tăng dần.

Input : 

9 3

9 5 2 8 51 4 46 98 100

Output : 5

Ý tưởng : 

Sắp xếp lại dãy theo chiều tăng dần, sau đó gọi ra Mang[k-1] để lấy vị trí thứ k

Độ khó thuật toán : O(NlogN – Trung bình)

2. Help Sudo

Sudo là 1 cậu bé rất thích chơi trốn tìm. Cậu thường rủ bạn bè chơi trên khu phố nơi có 1 hàng cây gồm n cái cây được cắt tỉa để chiều cao tăng dần. Sudo lại rất thích số x nên khi chơi cậu sẽ chốn ở cây có độ cao là x. Tuy nhiên hàng cây rất dài và Sudo đang rất khó khăn để tìm cây có chiều cao là x. Bạn hãy giúp Sudo nhé.

(Tìm xem có x tồn tại trong mảng không)

Input : 

5 16

2 4 7 9 16

Output : YES

Ý tưởng : Dùng lí thuyết tìm kiếm nhị phân để tìm xem có tồn tại số hay không

Độ khó thuật toán : O(logN)