Trong khoa học máy tính, chia để trị là một mô hình thiết kế thuật toán quan trọng, hoạt động dựa trên ý tưởng chia vấn đề cần giải quyết thành các vấn đề con cùng dạng với vấn đề đã cho, chỉ khác là cỡ của chúng nhỏ hơn, cứ như vậy lặp lại nhiều lần, cho đến khi bài toán thu được đủ đơn giản để có thể giải quyết trực tiếp. Sau đó, lời giải của các bài toán nhỏ được tổng hợp lại thành lời giải cho bài toán ban đầu.
Một giải thuật chia để trị thường được thiết kế theo 3 bước như sau:
- Chia (divide): Chia bài toán ra thành các bài toán nhỏ hơn (subproblems). Về cơ bản thì những bài toán nhỏ này giống với bài toán ban đầu.
- Trị (conquer): Giải quyết bài toán con trong trường hợp nó đủ nhỏ, còn không thì tiếp tục tiến hành chia tách nó ra thành những bài toán con nhỏ hơn nữa.
- Kết hợp (combine): Kết hợp các kết quả từ bài toán con nhỏ nhất, để ra lời giải cho các bài toán con (subproblems), và cứ thế cuối cùng ra được lời giải cho bài toán ban đầu.
- Áp dụng vào bài toán tính lũy thừa
Cách tính thông thường:
- Để tính a^b thì ta lặp từ 1 -> b rồi nhân dần a lên, độ phức tạp O(n)
VD: 3^5
Tính 1: 3×1 = 3
Tính 2: 3×3 = 9
Tính 3: 9×3 = 27
Tính 4: 27×3=81
Tính 5: 81×3=243
- Vậy mỗi bước, thực chất ta đang giảm bài toán từ a^b xuống thành a^(b-1) x a và lặp cho đến khi b về 0.
Thay vì đó, ta nhận thấy khi mũ b = 1 thì có thể đưa ra trực tiếp a, hoặc nếu mũ b bằng 0 thì đưa ra trực tiếp 1
Đồng thời tránh việc tràn số, ta sẽ mod các phép nhân theo công thức
Như vậy với mỗi lần đệ quy, ta sẽ chia bài toán về bài toán nhỏ hơn là a^(b/2) và tiếp tục như vậy cho đến khi đến điểm neo là b = 1 hoặc b = 0.
Độ phức tạp: O(logN)
- Áp dụng vào bài toán số Fibbonaci thứ N
Thông thường, với cách làm lặp/đệ quy và lưu vào mảng trước để thực hiện nhiều truy vấn, với n nhỏ ta hoàn toàn có thể làm điều đó với công thức f(n) = f(n-1) + f(n-2), tuy nhiên với những bài toán nàO(n) sẽ không thực hiện được trong thời gian giới hạn thì cách này sẽ không thể thực hiện được.
Nhận định:
- Liệu có thể đưa bài toán về dạng tính lũy thừa như ở trên rồi sử dụng chia để trị?
- Có thể tạo mối liên hệ giữa F(n) bất kì với các số trong dãy Fibbonaci không?
Cách làm theo tư tưởng chia để trị bằng cách áp dụng nhân ma trận:
Với 2 ma trận như sau:
Ma trận A :
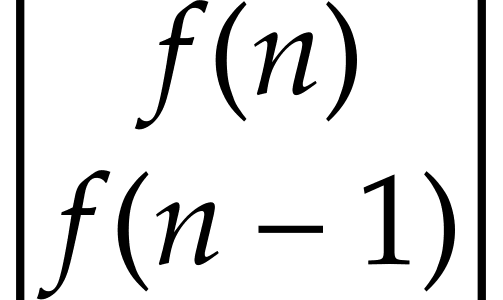
Ma trận B :
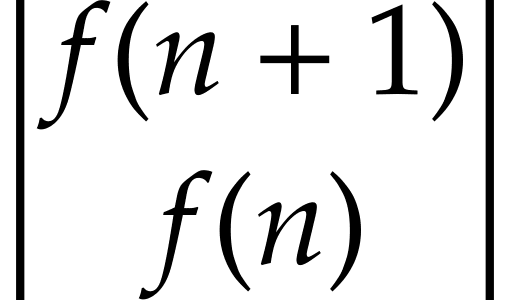
- Liệu có thể tìm thấy một ma trận X để B = X * A
Gọi ma trận cần tìm có dạng
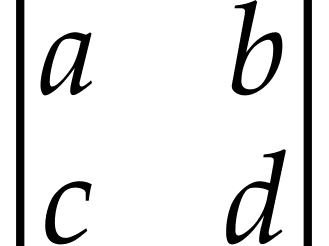
Thực hiện nhân hàng trên của ma trận, đồng thời f(n+1) = f(n) + f(n-1) ta có :
- a x f(n) + b x f(n-1) = f(n+1)
- a x f(n) + b x f(n-1) = f(n+1) = f(n) + f(n-1)
- a = 1, b = 1
Thực hiện nhân hàng dưới của ma trận, ta có:
- c x f(n) + d x f(n-1) = f(n)
- c = 1 , d = 0
Vậy ma trận X cần tìm có dạng
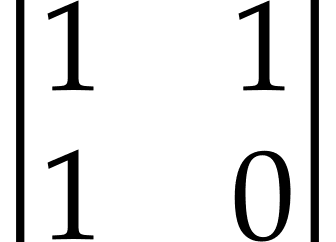
- Chứng minh quy nạp với các f(n) khác, ta có thể tìm được f(n) bất kì bằng cách nhân ma trận X với ma trận ban đầu (F(0) = 0, F(1) = 1)
- Hàm nhân 2 ma trận
- Lũy thừa ma trận áp dụng chia để trị
Tìm số Fibbonaci
