- Lý thuyết
Queue (Hàng đợi)
Hàng đợi (tiếng anh: Queue) là một cấu trúc dữ liệu dùng để lưu giữ các đối tượng theo cơ chế FIFO (viết tắt từ tiếng Anh: First In First Out), nghĩa là “vào trước ra trước”.
Có thể tưởng tượng queue như một hàng người xếp hàng, ai trên đầu thì vào trước, người tiếp tục xếp vào hàng sẽ vào sau theo thứ tự.
Các hàm có trong Queue:
- empty() Kiểm tra xem hàng đợi hiện tại có đang rỗng hay không.
- size() Trả về số lượng phần tử có trong hàng đợi
- front() Trả về phần tử đầu tiên của hàng đợi.
- back() Trả về phần tử cuối cùng của hàng đợi.
- push() Nạp thêm một phần tử vào hàng đợi (từ cuối)
- pop() Xóa một phần tử ở đầu của hàng đợi.
Tất cả các hàm trên có độ phức tạp O(1)
Priority Queue (Hàng đợi ưu tiên)
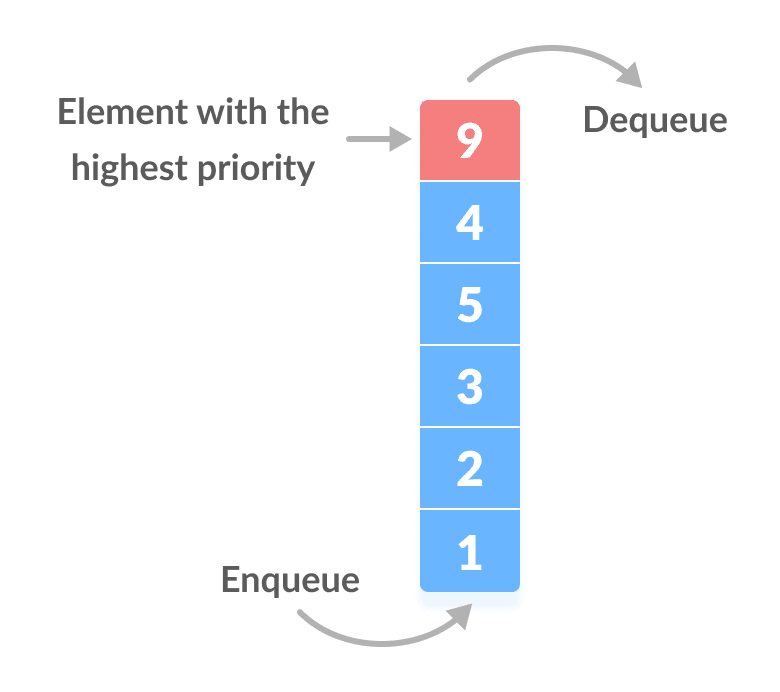
Đúng như cái tên của nó, hàng đợi ưu tiên là một phiên bản mở rộng của Queue (Hàng đợi) với các thuộc tính sau:
– Mọi phần tử đều được gắn liền với một độ ưu tiên
– Một phần tử có độ ưu tiên cao sẽ được dequeued (xóa khỏi Priority Queue) trước một phần tử có độ ưu tiên thấp
– Nếu hai phần tử có cùng độ ưu tiên, lúc này việc phần tử nào được xử lý trước sẽ phụ thuộc vào thứ tự của chúng ở trong Priority Queue.
Ví dụ: Phần tử có giá trị cao nhất được coi là phần tử có mức ưu tiên cao nhất. Tuy nhiên, trong các trường hợp khác, chúng ta có thể giả sử phần tử có giá trị thấp nhất là phần tử có mức ưu tiên cao nhất. Trong các trường hợp khác, chúng ta có thể thiết lập các mức ưu tiên tùy ý.
Sự khác biệt giữa Priority Queue và hàng đợi thông thường:
Trong một hàng đợi thông thường, quy tắc vào trước ra trước được thực hiện, trong khi đó, trong hàng đợi ưu tiên, các giá trị được lấy dựa trên cơ sở mức độ ưu tiên. Phần tử có mức ưu tiên cao nhất sẽ ra trước.
Có nhiều cách để triển khai Priority Queue, tuy nhiên trong thư viện chuẩn C++, cách thức được dùng là Heap vì Heap cung cấp thời gian trung bình tốt hơn các cách khác.
Cách thức hoạt động khi thêm phần tử:
Nếu không có nút,
Tạo một nút mới.
Mặt khác (một nút đã được tạo)
Chèn nút mới vào cuối (nút cuối cùng từ trái sang phải.)
Tạo cấu trúc dữ liệu heap cho mảng
Các lệnh của priority_queue trong thư viện STL của C++
empty() Kiểm tra hàng đợi có rỗng không O(1)
size() Trả về kích cỡ của hàng đợi O(1)
top() Trả về phần tử ưu tiên cao nhất của hàng đợi O(1)
push() Thêm một phần tử vào hàng đợi O(logN)
pop() Xóa phần tử ưu tiên cao nhất O(logN)
Với hàng đợi ưu tiên có N phần tử cần thêm vào thì chi phí khởi tạo là O(NlogN)
Deque (Hàng đợi hai đầu)
Hàng đợi hai đầu (deque) là cấu trúc dữ liệu chứa 0 hoặc nhiều phần tử có cùng kiểu dữ liệu và được biểu diễn bằng một hàng có phần tử đầu (front) và phần tử cuối (last). Deque hỗ trợ 4 thao tác như sau:
- Thêm một phần tử vào cuối deque. (Push back)
- Thêm một phần tử vào đầu deque. (Push front)
- Bỏ đi phần tử ở cuối deque, trả về giá trị của phần tử đó. (Pop back)
- Bỏ đi phần tử ở đầu deque, trả về giá trị của phần tử đó. (Pop front)
Về ứng dụng, ta sẽ bổ sung thêm một số thao tác sau:
- Lấy giá trị của phần tử cuối mà không xóa nó. (back)
- Lấy giá trị của phần tử đầu mà không xóa nó. (front)
- Tìm số lượng phần tử trong deque. (size)
- Kiểm tra xem deque có rỗng hay không. (empty)
Các thao tác trên đều có độ phức tạp khoảng O(1).
Bài tập ứng dụng
Chỉ đơn giản là sử dụng queue và làm theo yêu cầu của bài
Làm như cách làm của bài, tuy nhiên thay vì đẩy 2 phần tử của đầu queue xuống, ta sẽ lưu queue dưới dạng số-số lần xuất hiện, nếu như lần chơi hiện tại < số lần xuất hiện hiện tại, vậy thì đầu queue sẽ đang là số đó, bằng không ta đẩy số lần xuất hiện gấp đôi
VD : 1-1 2-1 3-1 4-1 5-1 (số – số lần xuất hiện)
Lượt chơi thứ 6: 1-2 2-2 3-2 4-2 5-2
