Mục tiêu
- + Sinh Nhị Phân
- + Sinh Tổ Hợp
- + Sinh Hoán Vị
- Sinh Nhị Phân

Nguyên lí hoạt động:
Bước 1: Chúng ta bắt đầu sinh với xâu rỗng “”
Bước 2: Tại mỗi lần sinh, ta đệ quy tiếp với xâu được thêm 1 và 0
Bước 3: Khi đạt đủ độ dài thì thêm vào vector toàn cục “kq”
Do mỗi lần sinh ta có 2 trường hợp và lặp như thế n lần, nên độ khó là O(2^n)
- Sinh Tổ Hợp
Nguyên lí hoạt động:
- Đầu tiên ta thử với index = 1, và số là 1. Sau đó cứ thử tiếp các trường hợp khác
- Chạy số 1 ->
- for (1->n) ra các số bắt đầu từ 1 -> ra các số bắt đầu từ 2,3,…
ra các số bắt đầu từ 2 -> ra các số bắt đầu từ 1,3,….
Độ khó: (n^k) Do mỗi lần ta cần đi qua n, và ta lặp tiếp n lần như thế cho đến khi đạt cấu hình k

- Sinh Hoán Vị
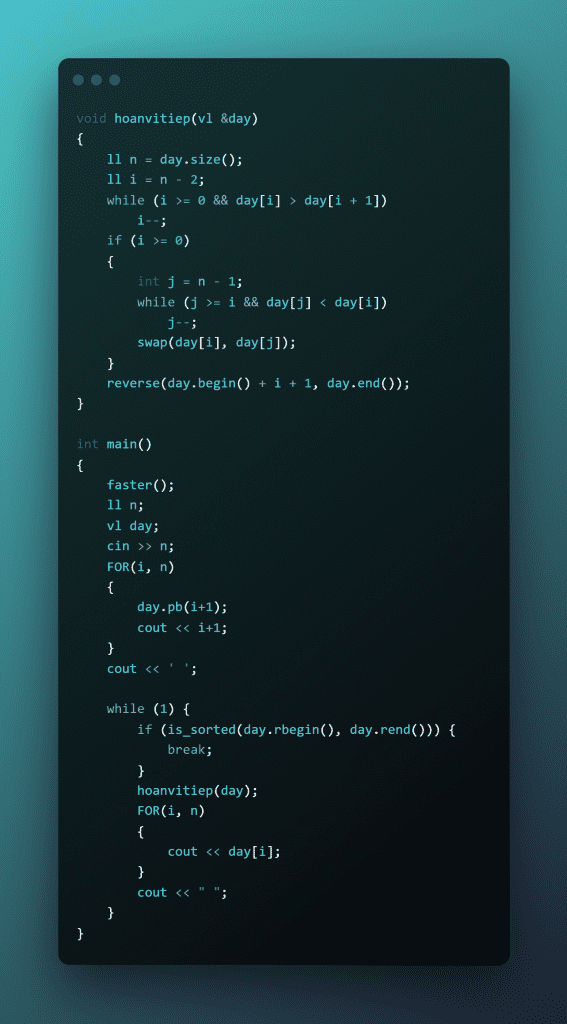
Nguyên lí hoạt động:
- Khởi tạo dãy ban đầu là 1..2..3….n
- Ta tiếp tục tìm hoán vị tiếp theo và in ra dãy hiện tại
Để tìm hoán vị tiếp theo:
- Hoán vị sinh ra phải lớn hơn hoán vị hiện tại hơn thế nữa phải là hoán vị vừa đủ lớn hơn hoán hoán vị hiện tại theo nghĩa không thể có một hoán vị nào khác chen giữa chúng khi sắp thứ tự.
- Vậy kỹ thuật sinh hoán vị kế tiếp từ hoán vị hiện tại được xây dựng như sau
+ Tìm từ vị trí sát cuối lên đầu, gặp chỉ số đầu tiên thỏa mãn x[i]<x[i+1] .
+ Nếu tìm thấy chỉ số i như trên
+ Trong đoạn cuối giảm dần, tìm phần tử x[k] nhỏ nhất thỏa mãn điều kiện x[k] >x[i].
+ Đảo giá trị x[k] và x[i]. Đảo ngược lại đoạn cuối
+ Nếu không tìm thấy tức là toàn dãy đã sắp xếp giảm dần, đây là cấu hình cuối cùng ( i < 0)
Độ khó: O(n!)
![[SWE học A.I] Phần 4: Machine Learning - Train & Test & Gradient Descent 1 image 18 - quochung.cyou PTIT](https://quochung.cyou/wp-content/uploads/2025/06/image-18-150x150.png)
![[SWE học A.I] Phần 3: Machine Learning Classification 2 image 13 - quochung.cyou PTIT](https://quochung.cyou/wp-content/uploads/2025/06/image-13-150x150.png)
![[SWE học A.I] Phần 2: Một số khái niệm toán học 3 image - quochung.cyou PTIT](https://quochung.cyou/wp-content/uploads/2025/06/image-150x150.png)
![[SWE học A.I] Phần 1: Machine Learning, Supervised Learning, Unsupervised Learning và Reinforment Learning 4 image 14 - quochung.cyou PTIT](https://quochung.cyou/wp-content/uploads/2025/05/image-14-150x150.png)





![[SWE học A.I] Phần 4: Machine Learning - Train & Test & Gradient Descent 36 image 18 - quochung.cyou PTIT](https://quochung.cyou/wp-content/uploads/2025/06/image-18.png)
![[SWE học A.I] Phần 3: Machine Learning Classification 37 image 13 - quochung.cyou PTIT](https://quochung.cyou/wp-content/uploads/2025/06/image-13.png)
![[SWE học A.I] Phần 2: Một số khái niệm toán học 38 image - quochung.cyou PTIT](https://quochung.cyou/wp-content/uploads/2025/06/image.png)
![[SWE học A.I] Phần 1: Machine Learning, Supervised Learning, Unsupervised Learning và Reinforment Learning 39 image 14 - quochung.cyou PTIT](https://quochung.cyou/wp-content/uploads/2025/05/image-14.png)