- Lý thuyết
Stack là một danh sách được bổ sung 2 thao tác: thêm một phần tử vào cuối danh sách, và loại bỏ một phần tử ở cuối danh sách. Ví trí cuối của Stack được gọi là đỉnh (top).
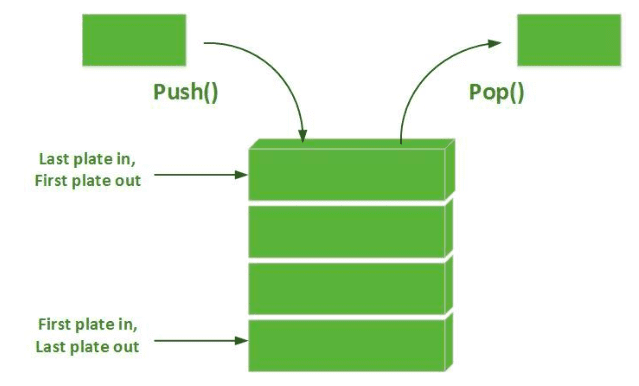
Stack và Queue là các cấu trúc dữ liệu được sử dụng để lưu trữ các yếu tố dữ liệu và nó dựa trên một số các ví dụ có thực trong cuộc sống hàng ngày của chúng ta. Ví dụ, Stack là một chồng đĩa CD, nơi bạn có thể lấy ra và đưa vào đĩa CD thông qua đỉnh của ngăn xếp đĩa CD.
Chủ yếu Stack có ba hàm cơ bản sau được thực hiện:
- Push: Thêm một mục(phần tử, thành phần) trong stack. Nếu stack đầy, thì nó được cho là điều kiện Tràn.
- Pop: Loại bỏ một mục khỏi stack. Các mục được xuất hiện theo thứ tự đảo ngược mà chúng được Push. Nếu stack trống, thì nó được cho là điều kiện trống.
- Peek hoặc Top: Trả về phần tử trên cùng của stack.
- isEmpty: Trả về true nếu stack trống, ngược lại là false.
Tất cả các hàm trên của stack đều có độ phức tạp O(1)
BÀI TẬP ỨNG DỤNG : Tìm Min/Max trên đoạn tịnh tiến
Sơ lược đề bài: Cho một dãy số có n phần tử, in ra max của các đoạn có độ dài k liên tiếp trong dãy
Cách làm thông thường:
Ta lặp từ 1-> n, với mỗi đoạn k, ta lặp qua đoạn k và lấy phần tử min, max.
Độ phức tạp: O(N*k)
Sử dụng stack:
- Trước hết ta tìm phần tử lớn hơn nó bên phải đầu tiên
- Đặt 1 biến j và i. Tại mỗi vị trí kiểm tra, ta lặp tìm phần tử lớn nhất bên phải mà vẫn thuộc vùng (i+k-1)
- Chạy chay: (k = 3). A = (1, 2, 3, 1, 4, 5, 2, 3, 6)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 2 | 3 | 1 | 4 | 5 | 2 | 3 | 6 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 2 | 4 | 4 | 5 | 8 | 8 | 8 | 9 |
| 2 | 3 | 4 | 4 | 5 | 6 | 6 | 6 | X |
0: (i+k-1) = 2. Trong vùng vị trí (0-2) có các vị trí phần tử lớn hơn là (1,2,4) có 1-2 thỏa mãn, lấy vị trí 2 -> 3
1: (i+k-1) = 3. Trong vùng (1-3) phần tử lớn hơn phải là: (2,4,4) , có vị trí 2 thỏa mãn, lấy vị trí 2-> 3
2: (i+k-1) = 4. Trong vùng (2-4), phần tử lớn hơn bên phải lả (4,4,5), có vị trí 4 thỏa mãn, lấy 4 -> 4
…
Kết quả: 3 3 4 5 5 5 6
![[SWE học A.I] Phần 8: Model Training & Evaluation 1 image 18 - quochung.cyou PTIT](https://quochung.cyou/wp-content/uploads/2025/06/image-18-150x150.png)
![[SWE học A.I] Phần 7: Overfit & Underfit, Tradeoff của Variance/Bias 2 image 63 - quochung.cyou PTIT](https://quochung.cyou/wp-content/uploads/2025/06/image-63-150x150.png)
![[SWE học A.I] Phần 6: Machine Learning Classification 3 image 13 - quochung.cyou PTIT](https://quochung.cyou/wp-content/uploads/2025/06/image-13-150x150.png)
![[SWE học A.I] Phần 4: Data Prepare & Cleaning 4 image 71 - quochung.cyou PTIT](https://quochung.cyou/wp-content/uploads/2025/06/image-71-150x150.png)
![[SWE học A.I] Phần 3: Một số khái niệm suất thống kê 5 image 44 - quochung.cyou PTIT](https://quochung.cyou/wp-content/uploads/2025/06/image-44-150x150.png)
![[SWE học A.I] Phần 2: Một số khái niệm toán học 6 image - quochung.cyou PTIT](https://quochung.cyou/wp-content/uploads/2025/06/image-150x150.png)
![[SWE học A.I] Phần 1: Sơ lược tiếp cận các mô hình A.I 7 image 14 - quochung.cyou PTIT](https://quochung.cyou/wp-content/uploads/2025/05/image-14-150x150.png)


![[SWE học A.I] Phần 8: Model Training & Evaluation 26 image 18 - quochung.cyou PTIT](https://quochung.cyou/wp-content/uploads/2025/06/image-18.png)
![[SWE học A.I] Phần 7: Overfit & Underfit, Tradeoff của Variance/Bias 27 image 63 - quochung.cyou PTIT](https://quochung.cyou/wp-content/uploads/2025/06/image-63.png)
![[SWE học A.I] Phần 6: Machine Learning Classification 28 image 13 - quochung.cyou PTIT](https://quochung.cyou/wp-content/uploads/2025/06/image-13.png)
![[SWE học A.I] Phần 4: Data Prepare & Cleaning 29 image 71 - quochung.cyou PTIT](https://quochung.cyou/wp-content/uploads/2025/06/image-71.png)